Protein isoelectric point calculator
Isoelectric point definition:
Isoelectric point (pI) is a pH in which net charge of protein is zero. In case of proteins isoelectric point mostly depends on seven charged amino acids: glutamate (δ-carboxyl group), aspartate (ß-carboxyl group), cysteine (thiol group), tyrosine (phenol group), histidine (imidazole side chains), lysine (ε-ammonium group) and arginine (guanidinium group). Additionally, one should take into account charge of protein terminal groups (NH2 i COOH). Each of them has its unique acid dissociation constant referred to as pK.Moreover, net charge of the protein is in tight relation with the solution (buffer) pH. Keeping in main this we can use Henderson-Hasselbach equation to calculate protein charge in certain pH:
- for negative charged residues:
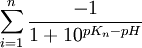
where pKn is the acid dissociation constant of negatively charged amino acid
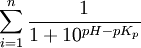
where pKp
is the acid dissociation constant of positively charged amino acid
As you can see, only pH of buffer is variable in equations. If we successively change this value, finally we will find isoelectric point of analyzed protein.
The knowledge of isoelectric point is of great significance in biochemistry (mainly in elecrophoresis and isofocusing techniques), because it allows to match proper environment before
the experiment starts.
Generally, macromolecules are positively charged and on the other hand, above proteins isoelectric point,
their charge is negative. For example, during electrophoresis, direction of proteins migration, depends only from their charge. If buffer pH (and as a result gel pH) is
higher than protein isoelectric point, the particles will migrate to the anode (negative electrode) and if the buffer pH is lower than isoelectric point they will go to the cathode.
In situation when the gel pH and the protein isoelectric point are equal, proteins do not move at all.
Using above formulas, we can calculate theoretical isoelectric point. The result will be almost surely different than real isoelectric point. It is mainly because many proteins are chemically modified (amino acids can be phosphorylated, methylated, acetyleted etc.), which change their charge. Problematic is also the occurrence of cysteines (negative charge) which can oxidise and form disulfide bond in protein. Therefore, they will become cystines, which do not express any charge.
Nevertheless, one can approximately calculate protein isoelectric point which is ± 0.5 of exact isoelectric point. The most critical moment during isoelectric point determination is usage of appropriate pK values. Unfortunately, there is no agreement in this matter. Each source gives different pKs. Some of them are presented below:
Using above formulas, we can calculate theoretical isoelectric point. The result will be almost surely different than real isoelectric point. It is mainly because many proteins are chemically modified (amino acids can be phosphorylated, methylated, acetyleted etc.), which change their charge. Problematic is also the occurrence of cysteines (negative charge) which can oxidise and form disulfide bond in protein. Therefore, they will become cystines, which do not express any charge.
Nevertheless, one can approximately calculate protein isoelectric point which is ± 0.5 of exact isoelectric point. The most critical moment during isoelectric point determination is usage of appropriate pK values. Unfortunately, there is no agreement in this matter. Each source gives different pKs. Some of them are presented below:
| Amino acid | NH2 | COOH | C | D | E | H | K | R | Y |
| EMBOSS | 8.6 | 3.6 | 8.5 | 3.9 | 4.1 | 6.5 | 10.8 | 12.5 | 10.1 |
| DTASelect | 8.0 | 3.1 | 8.5 | 4.4 | 4.4 | 6.5 | 10.0 | 12.0 | 10.0 |
| Solomon | 9.6 | 2.4 | 8.3 | 3.9 | 4.3 | 6.0 | 10.5 | 12.5 | 10.1 |
| Sillero | 8.2 | 3.2 | 9.0 | 4.0 | 4.5 | 6.4 | 10.4 | 12.0 | 10.0 |
| Rodwell | 8.0 | 3.1 | 8.33 | 3.68 | 4.25 | 6.0 | 11.5 | 11.5 | 10.07 |
| Patrickios | 11.2 | 4.2 | - | 4.2 | 4.2 | - | 11.2 | 11.2 | - |
| Wikipedia | 8.2 | 3.65 | 8.18 | 3.9 | 4.07 | 6.04 | 10.54 | 12.48 | 10.46 |
| Lehninger | 9.69 | 2.34 | 8.33 | 3.86 | 4.25 | 6.0 | 10.5 | 12.4 | 10.0 |
| Grimsley1 | 7.7 | 3.3 | 6.8 | 3.5 | 4.2 | 6.6 | 10.5 | 12.04 | 10.3 |
| Toseland | 8.71 | 3.19 | 6.87 | 3.6 | 4.29 | 6.33 | 10.45 | 12.0 | 9.61 |
| Thurlkill | 8.0 | 3.67 | 8.55 | 3.67 | 4.25 | 6.54 | 10.4 | 12.0 | 9.84 |
| Nozaki_Tanford | 7.5 | 3.8 | 9.5 | 4.0 | 4.4 | 6.3 | 10.4 | 12.0 | 9.6 |
| Dawson2 | 8.2 | 3.2 | 8.3 | 3.9 | 4.3 | 6 | 10.5 | 12.0 | 10.0 |
| Bjellqvist3 | 7.5 | 3.55 | 9.0 | 4.05 | 4.45 | 5.98 | 10.0 | 12.0 | 10.0 |
| IPC_protein | 9.094 | 2.869 | 7.555 | 3.872 | 4.412 | 5.637 | 9.052 | 11.84 | 10.85 |
| IPC_peptide | 9.564 | 2.383 | 8.297 | 3.887 | 4.317 | 6.018 | 10.517 | 12.503 | 10.071 |
1 Arg was not included in the study and the average pK from all other scales was taken
2 NH2 and COOH were not included in the study and they were taken from Sillero
3 Bjellqvist model include also different pK values for terminal residues
More advanced algorithm, implemented in ProMoST, takes into account localization of the charged amino acid:
| aa | N term | middle | C term |
| K R H D E C U* Y |
10.00 11.50 4.89 3.57 4.15 8.00 5.20 9.34 |
9.80 12.50 6.08 4.07 4.45 8.28 5.43 9.84 |
10.30 11.50 6.89 4.57 4.75 9.00 5.60 10.34 |
| * pK was taken from Byun et al. 2011 | |||
| aa | N | C | aa | N | C | aa | N | C | aa | N | C | |||
| G A S P |
7.50 7.58 6.86 8.36 |
3.70 3.75 3.61 3.61 |
V T I L |
7.44 7.02 7.48 7.46 |
3.69 3.57 3.72 3.73 |
N Q M F |
7.22 6.73 6.98 6.96 |
3.64 3.57 3.68 3.98 |
W X* Z** B*** |
7.11 7.26 6.96 7.46 |
3.78 3.57 3.54 3.57 | |||
| * X - average from all amino acids ** Z =(E+Q)/2 *** B =(N+D)/2 | ||||||||||||||
If you are interested in the implementation site of IPC, the old version can be accessed here. At the beginning it was written in C++, and in given link some information with sources code is available for educational purposes (this is old code so fairly naive, and not well cleaned, but additionally you can find there GUI for windows, some tips for implementation etc.).
Contact: Lukasz P. Kozlowski